Improving Amine Regenerator Convergence
Luke Addington
October 23, 2007
Amine systems can be tough to calculate. However, there are a few things that you can do to help out. In this post we're going to discuss a few options on the convergence tab, especially the Enthalpy Model and the Inner Loop Model.
The amine regenerator can, at times, be especially challenging. Sometimes the column will refuse to converge or will converge quite slowly. A few select components with non-ideal volatilities such as ammonia can make things especially tough. Below is some general information about the various options and some best practices to use while working with your model. These parameters can be found on the "Column Convergence" Tab in ProMax.
Enthalpy Model
Boston-Britt - is selected by default and calculates the total molar enthalpy for each of the phases on each stage as a function of temperature only. As there is only one variable, iterations for this method are very fast.
The Composition-Dependent - method is more rigorous than Boston-Britt and calculates the partial molar enthalpy in the liquid phase for each of the reactive components in an electrolytic system, or all components in a non-electrolytic system. This method can help convergence issues, especially in cases where the composition changes significantly with each outer loop calculation.
Inner-Loop Model
The Boston-Sullivan - Loop Model is selected by default and linearizes the enthalpy and volatility during column calculation. The number of variables in the inner loop is thus reduced to the number of stages plus the number of specifications in the column.
Boston-Sullivan Non-Ideal - is a more rigorous inner loop method. Instead of linearizing enthalpy and volatility, this method calculates partial molar liquid fugacity for each component in non-electrolytic systems or for each reactive component in electrolytic systems.
As an example, let's take the case of an amine regenerator containing ammonia. If you run this column with the default settings you will likely have difficulty with convergence. In real column operation, these units have a tendency to build up ammonia in the overhead loop due to the volatility profile of ammonia and the column operating temperatures. If you watch the flow rates on each stage, or the overhead loop, during the column convergence you will notice a similar build up in ProMax. Perhaps the first outer-loop showed 0.1% NH4 in the overhead. The next loop showed 0.2%, then 0.5%, then 1% and so on. This is a pretty sizable change in the composition for each loop, so Boston-Britt may not be the best Enthalpy Model to use. Composition-Dependent would give you a more accurate enthalpy for each iteration as it takes the changing composition into account and would thus help with convergence.
Now that we set the enthalpy model to Composition-Dependent we see that the column gets a little closer to convergence, but still solves to an approximate solution at the end. Perhaps we should take a look at the Inner-Loop model.
Below is a graph of the volatility of ammonia as a function of temperature. We should note standard temperatures for amine regenerators are around 50˚C for the condenser and around 120˚C at the reboiler.
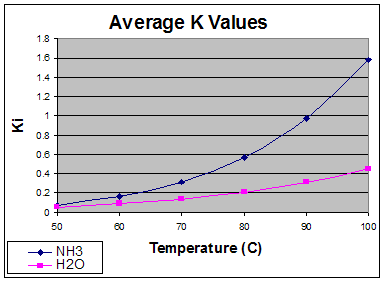
Looking at the graph, making the volatility linear may not be a good idea. While the column may at times converge without the Inner-Loop model set to Boston-Sullivan, it will almost certainly converge with fewer steps with Boston-Sullivan non-ideal.
There is a trade-off, of course, using these settings. While we have fewer iterations, we have greatly increased the number of variables and thus the speed of calculating each iteration. This is why Boston-Britt and Boston-Sullivan are selected by default; they are the fastest settings available. But in cases where the column does not converge well with these two, it may be faster--or necessary--to use a different combination to get our solution.
It should be noted that none of these settings affect the actual solution. They are merely the approach taken to calculate the column. The end result is still a function of the thermodynamic package chosen.
Review Issues with Column Convergence
Authored by Luke Addington (BR&E Sales)